
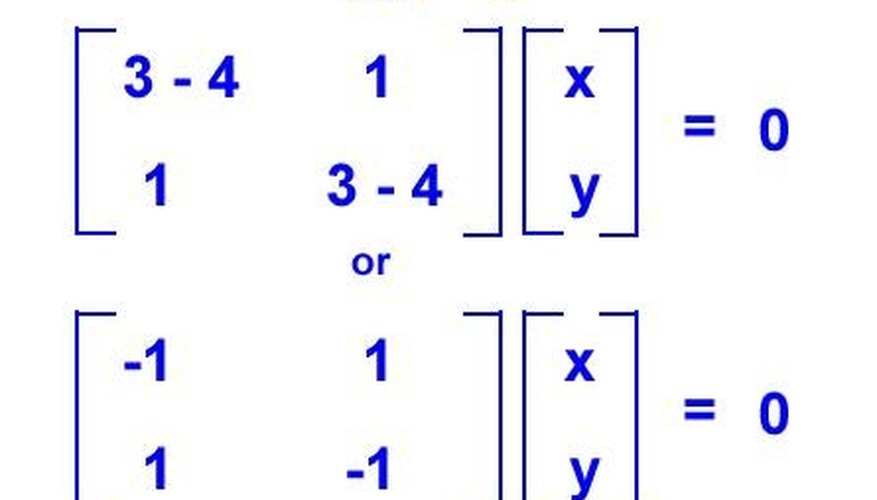
# import required libraryĪ = torch.randn(2,2, dtype = torch.cfloat ) In this program, we compute eigenvalues and eigenvectors of a square complex matrix. Wikipedia brings the following definition: In linear algebra, the singular-value decomposition (SVD) is a factorization of a real or complex matrix. It will produce the following output − Matrix: Answer (1 of 4): It is possible to decompose an m times n matrix with a generalization of eigendecomposition called Singular Value Decomposition. Print("Eigen Vectors:\n", eigenvectors) Output # compute the Eigen values and vectors of the matrix In this program, we compute the eigenvalues and eigenvectors of a square matrix. Print("Eigen Vectors:\n", eigenvectors) Example 1 Of course, finding the transform is a challenge. We say that the transform diagonalizes'' the matrix. Each eigenvalue is paired with a corresponding set of so-called eigenvectors. ) This solves the problem, because the eigenvalues of the matrix are the diagonal values in, and the eigenvectors are the column vectors of. Eigenvalues (translated from German, meaning 'proper values') are a special set of scalars associated with every square matrix that are sometimes also known as characteristic roots, characteristic values, or proper values. Here A is square matrix.Įigenvalues, eigenvectors = (A) (An orthogonal matrix is one whose transpose is its inverse. Ĭompute Eigen value decomposition of square matrix or batch of square matrices using (A). Here we define a square matrix (a 2D torch tensor) of size. Make sure you have already installed it.Ĭreate a square matrix or batch of square matrices. The solutions of the eigenvalue equation are the eigenvalues of X. Then, solve the equation, which is the det (X I) 0, for. Now, write the determinant of the square matrix, which is X I. In other words, here we use intra- image distances. To find the eigenvalues of a 3×3 matrix, X, you need to: First, subtract from the main diagonal of X to get X I. In all the following examples, the required Python library is torch. A square proximity matrix H is created, recording the distances between features within the image. It returns a named tuple (eigenvalues, eigenvectors).
#Eigenvalue squeed matrix squared free
Eigenvalue of a square matrix - definition of eigenvalue of a square matrix by The Free Dictionary.
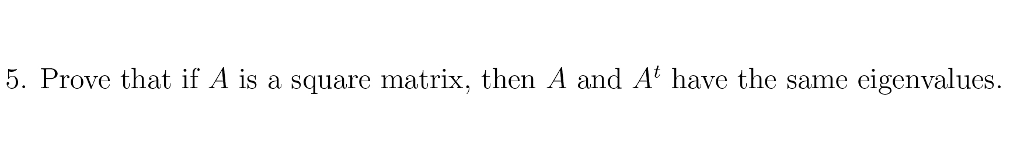
Where A is a square matrix or a batch of square matrices. eigenvalue of a square matrix - any number such that a given square matrix minus that number times the identity matrix has a zero determinant. The eigenvectors are given by columns of eigenvectors. The eigenvalues and eigenvectors are always complex valued.

It accepts matrix and batch of matrices of float, double, cfloat and cdouble data types. Such that \(S_\).() computes the Eigen value decomposition of a square matrix or a batch of square matrices. ¡Consulta la traducción inglés-alemán de eigenvalue of a square matrix en el diccionario en línea PONS Entrenador de vocabulario, tablas de conjugación, opción audio gratis. 1 t min x x >o where the minimum is taken over the eigenvalues of E(0). Quantum object: dims =, ],, ]], shape = (4, 4), type = super, isherm = Falseįor qubits, a particularly useful way to visualize superoperators is to plot them in the Pauli basis, Generating Random Quantum States & Operators.

Visualization of quantum states and processes.numbers behave for large n for real or complex and square or rectangular matrices. So, A is similar to a diagonal matrix D and entries of the main diagonal of D are the eigenvalues of A. Estimate the unconditional correlation matrix and use it for. It is, assuming the square of the absolute value of the eigenvalue of the arbitrary unitary operator Im analyzing equals 1. If A is a real symmtric matrix, then it is diagonalisable and its eigenvalues are real. Time Evolution and Quantum System Dynamics Given a random matrix, what condition number should be expected. is to correct in-sample biases of sample covariance matrix eigenvalues a favored model.Using Tensor Products and Partial Traces.Choi, Kraus, Stinespring and \(\chi\) Representations.Superoperators and Vectorized Operators.


 0 kommentar(er)
0 kommentar(er)
